AN00: Shot Noise Limit of the DPD80 1550nm
This application note examines the shot noise limit of the DPD80 1550nm and compares it to the shot noise limit of the New Focus 1811 photodetector.
What is shot noise?¶
When photons collide with the surface of a photodiode the random statistical fluctuations in collision rate, due to the discrete nature of photons, is a source of noise. The arrival rate of photons can be modelled with a Poisson distribution, meaning the photons arrive at an average constant rate, but the probability of each photon arriving at a given time is independent of the other photons. The noise that is generated is called shot noise. The power spectral density (PSD) of shot noise measured by a photodetector is
where \(S(f)\) is the single-sided PSD having units of \(\mathsf{W}^2 / \mathsf{Hz}\). Shot noise is constant across frequency and a fundamental lower limit of the noise floor in most optics experiments. Shot noise depends on photon energy, \(h\nu\), the average incident optical power of the light source, \(\bar{P}\), and the quantum efficiency of the detector, \(\eta_q\). The total noise measured by a photodetector is the addition in quadrature of the photodetector noise and shot noise. At optical powers where the shot noise is the dominant noise source, the photodetector is said to be shot noise limited.
Note that when a quantum efficiency of 100% is assumed, \(\eta_q = 1\), equation (1) reduces to
analogous to the Schottky formula for electrical shot noise [1] [2], equation (4), and as reported elsewhere as the PSD for optical shotnoise [3].
Measurements¶
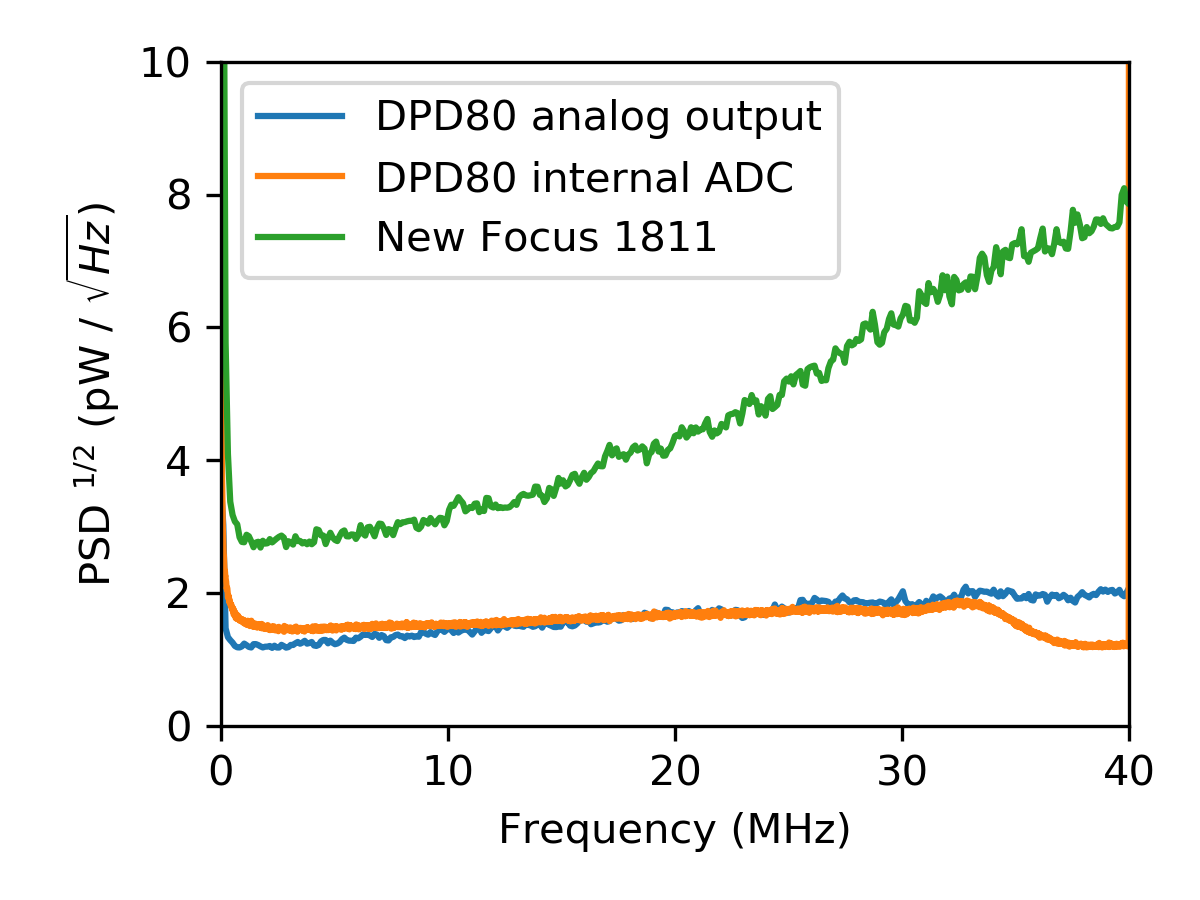
The noise floor of both the Resolved Instruments DPD80 USB photodetector and the New Focus 1811 photodetector were measured with no light incident on their photodiodes, and is plotted in Fig. 1. As can be seen, the DPD80’s noise floor is much lower and flatter across frequency than the New Focus 1811’s revealing the DPD80 USB Photodetector will be shot noise limited at lower optical powers.
Fig. 1 Noise floor comparison between the DPD80 in high gain mode and the New Focus 1811.
Shot noise was observed by shining a constant optical power (30.1 μW at 1550 nm) on the DPD80’s photodiode (Fig. 2), causing an increase in the noise floor across frequencies–consistent with the spectrally white nature of shot noise. To compare the measured noise with the expected contribution of shot noise, the “calculated shot noise” in Fig. 2 was found using equation (1) and added in quadrature to the initial noise-floor measurement. This calculated noise matches the measured contribution from the shot-noise well.
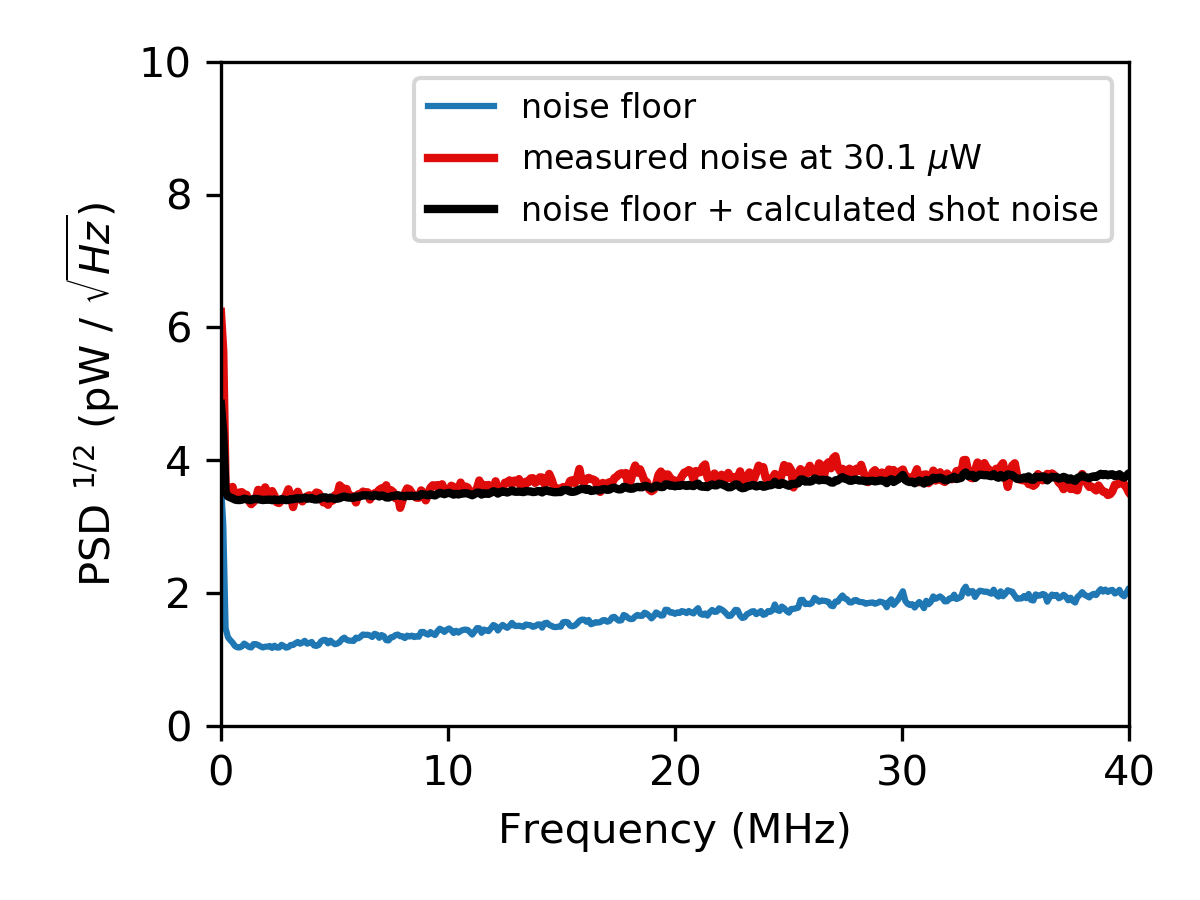
Fig. 2 Measurements showing the increase in the noise floor from the shot noise at 30.1 μW, compared to the expected noise using equation (1).
The minimum optical power at which a photodetector is shot noise limited, \(\bar{P}_{min}\), can be found by solving equation (2) for power and by letting the PSD be equal to the photodetector’s noise equivalent power (\(S_\mathsf{NEP}\)):
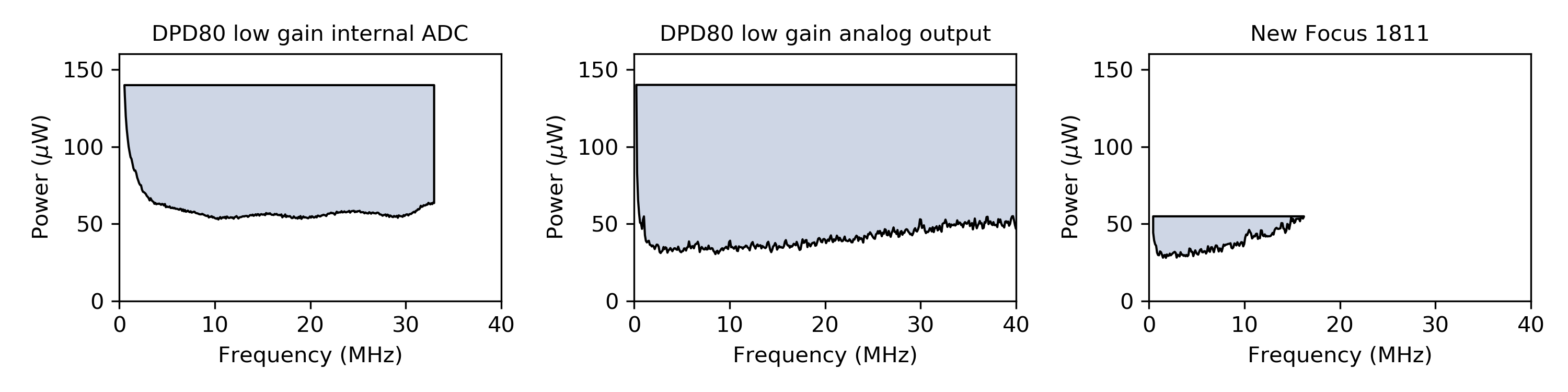
This equation is a lower limit to the powers at which a photodetector is shot-noise limited. Equation (2) was chosen instead of equation (1) as it provides a more conservative calculation of the shot-noise limit. The upper limit of powers is given by the saturation power of the photodetector. In Fig. 3 (Fig. 4) the shot noise limited region of the DPD80 in high gain (low gain) mode is compared to the New Focus 1811.
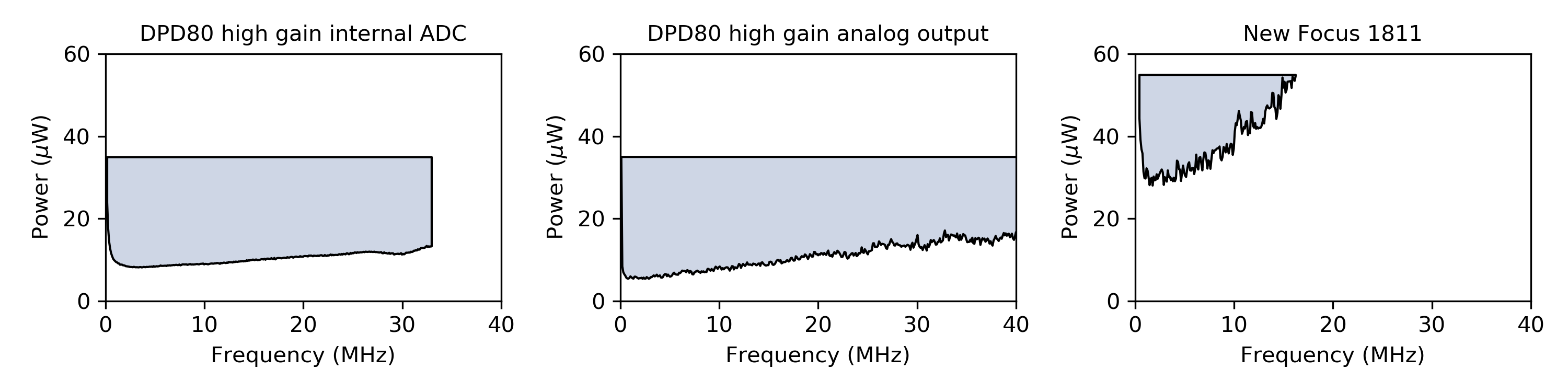
Fig. 3 The shot noise limited regions of the DPD80 in high gain mode compared to the New Focus 1811.
Fig. 4 The shot noise limited regions of the DPD80 in low gain mode compared to the New Focus 1811.
Fig. 3 shows that the DPD80 USB Photodetector is shot noise limited at optical powers above approximately 10 μW, whereas the New Focus 1811 is only shot noise limited above approximately 30 μW. Additionally, the DPD80’s flat noise floor enables shot noise limited measurements across a much wider frequency range. In low gain mode, the saturation power of the DPD80 is increased with a trade-off of increasing the noise floor. This permits shot noise limited measurements up to the saturation power of 140 μW.
Thank you for reading this application note. If you have any questions or comments please email us at info@resolvedinstruments.com
Appendix¶
Shot noise derivation¶
To derive equation (1), we initially start with the Schottky formula for electronic shot noise [1] [2]:
where \(S_I(f)\) is the single sided PSD for current noise in units of \(\mathsf{Amps}^2 / \mathsf{Hz}\), \(e\) is the electron charge, and \(\bar{I}\) is the mean current. Since a photodiode produces a current, equation (4) can be considered the current shot-noise produced by the photodiode.
To find the equivalent shot-noise in units of optical power due to the incident light on the photodiode, we must consider the responsivity of the photodiode, \(R_\nu\), which gives a measure of the electrical current produced by the photodiode per unit optical power incident on the photodiode:
with \(\eta_q\) being the quantum efficiency of the photodiode, \(\nu\) the frequency of photon being measured, and \(h\) being Planck’s constant.
Using this ratio the equivalent shot-noise in optical power can be found with
noting \(\bar{I}/R_\nu = \bar{P}\) and expanding the other \(R_\nu\) we find
the shot-noise in terms of optical power incident on the photodiode in units of \(\mathsf{W}^2 / \mathsf{Hz}\).
Methods¶
The analog signals were measured using a Zurich Instruments HF2LI lock-in amplifier, and the digital data measurements with the DPD80 were streamed via USB 3.0 directly to a computer. The frequencies that could be examined in this application note were limited by the bandwidth of the HF2LI. The light source for the shot noise in Fig. 2 was a Newport TLB-6730 tunable laser set at 1550 nm. The measurements using the Newfocus 1811 photodetector were calibrated by matching the power of an optical tone at 1 MHz to the same signal measured by a calibrated DPD80 USB Photodetector.